How to Write Merge Sort from Scratch

Want to remember at least one sorting algorithm that is actually used in programming libraries? Merge sort is simpler than you think, all the code is in the article.

In this article, I’d like to tell you about merge sort and will walk you through its implementation. All the code can be found here.

Why This Algorithm?

Despite being a pretty old making (over 70 years) this comparison-based algorithm is still used in programming libraries, for a reason of course — it is still competitive performance-wise: O(nlogn). As a relevant example for Java world developers check out the Java doc of Arrays.sort().

High Level of How It Works

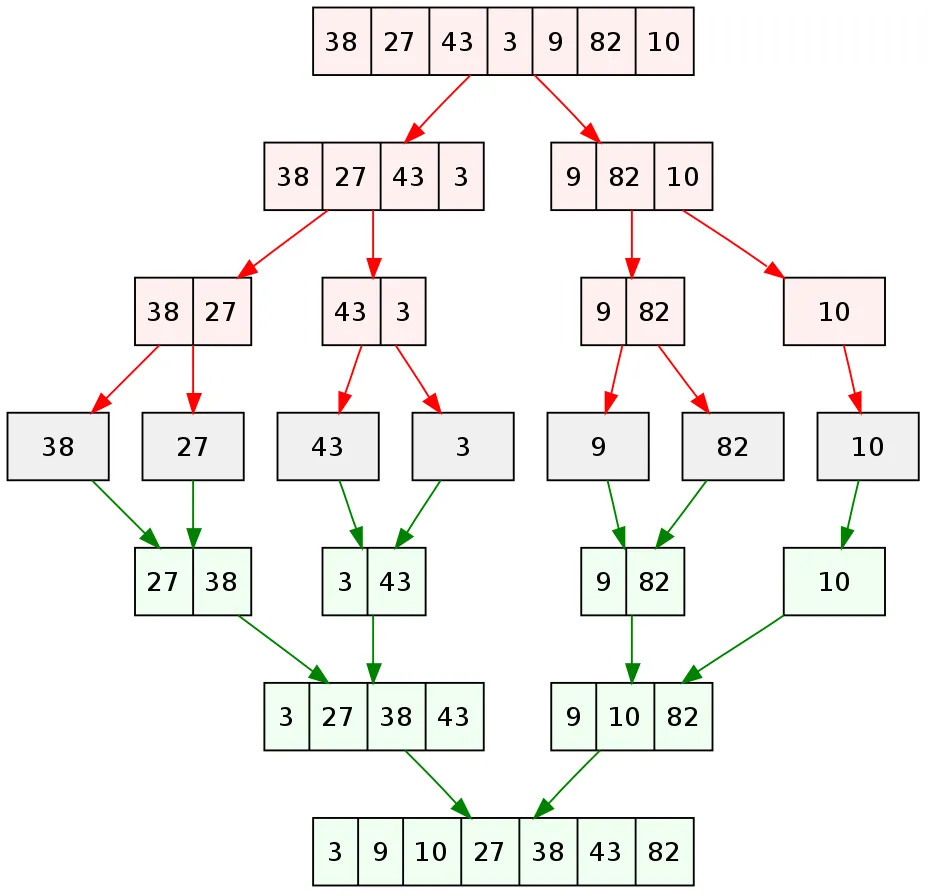
Merge sort is a canonical example of a “divide and conquer” algorithm, which means it breaks down a problem into smaller subproblems, recursively solves them, and combines the solutions. What it means for the case of array sorting is better to illustrate visually first:

We split the incoming array into halves (not strictly when the size of the array is odd) until they reach the moment when sorting is no longer required — a single-element array. This stage is displayed in a row of grey cards in the picture above. After that, we merge halves into small sorted arrays until we reach the last merge which will result in a sorted version of our initial input array. If not clear I’d suggest taking a look at this visualization.

Let’s code

Merge subroutine

If you noticed in the high-level description the most complicated part of the algorithm is merging — when we receive two sorted arrays and need to make out of them one sorted array. Let’s do this “heavy lifting” first and leave the recursive part for dessert.

fun merge(firstArray: IntArray, secondArray: IntArray): IntArray {
    val resultingArray = IntArray(firstArray.size + secondArray.size)
    var firstArrayPointer = 0
    var secondArrayPointer = 0
    for (resultingArrayPointer in resultingArray.indices) {
        if (firstArray[firstArrayPointer] <= secondArray[secondArrayPointer]) {
            resultingArray[resultingArrayPointer] = firstArray[firstArrayPointer]
            firstArrayPointer++
        } else {
            resultingArray[resultingArrayPointer] = secondArray[secondArrayPointer]
            secondArrayPointer++
        }
    }
    return resultingArray
}

Here we create an empty resulting array first, its size would be a sum of the sizes of input arrays. Then we iterate this resulting array in order to fill it by taking the smallest remaining element from both of the input arrays.

As an example let’s take a look at one of the merges from the pic above: [27,38] and [3,43]. We create a resulting array of size 4 and in order to fill its first element we compare the first elements of both inputs — as a result, 3 is the smallest element and going to be the first element in the resulting array. To fill the next element in the resulting array we check again, but this time we skip 3 in the second input as it was already taken, 27 is taken now and the same way in the next iterations 38 and 43 will be added to the resulting array.

We are almost done here, just look at the code again — especially how we use indices of input arrays. Will we get in any trouble if we are to receive [1,2] and [3,4] as input? Right, we are going to get our IndexOutOfBoundException when both of the elements of the first array jump in the resulting array while the second one stays “untouched”. In this case, we can introduce a simple check for both of the indices, if one of them reaches the end of the array, copy the remaining of the other input array to the resulting one and finish merging. In our example when we will see that both 1 and 2 are copied then we will copy [3,4] straight away and no more iterations would be needed. Here is the code:

if (firstArrayPointer == firstArray.size) {
    secondArray.copyInto(
        resultingArray,
        destinationOffset = resultingArrayPointer,
        startIndex = secondArrayPointer
    )
    return resultingArray
}
if (secondArrayPointer == secondArray.size) {
    firstArray.copyInto(
        resultingArray,
        destinationOffset = resultingArrayPointer,
        startIndex = firstArrayPointer
    )
    return resultingArray
}

Recursion fun

Now the easy part, we are doing an array split in halves, call it recursively, and merge the results. This just works like magic:

fun sort(inputArray: IntArray): IntArray {
    val size = inputArray.size
    return if (size == 1 || size == 0) {
        inputArray
    } else {
        val firstHalfOfInputArraySorted = sort(inputArray.copyOfRange(0, size / 2))
        val secondHalfOfInputArraySorted = sort(inputArray.copyOfRange(size / 2, size))
        merge(firstHalfOfInputArraySorted, secondHalfOfInputArraySorted)
    }
}

Check results

Let’s check it on several different input arrays to see how well we implemented it.

fun main() {
    println(sort(intArrayOf()).toList())  // []
    println(sort(intArrayOf(3)).toList()) // [3]
    println(sort(intArrayOf(3, -1)).toList()) // [-1, 3]
    println(sort(intArrayOf(0, 5, 3, 4, 7)).toList()) // [0, 3, 4, 5, 7]
    println(sort(intArrayOf(0, 5, 3, 4, 7, 6)).toList()) // [0, 3, 4, 5, 6, 7]
    println(sort(intArrayOf(6, 5, 4, 3, 2, 1)).toList()) // [1, 2, 3, 4, 5, 6]
    println(sort(intArrayOf(0, 0, 1, 1, 0, 0)).toList()) // [0, 0, 0, 0, 1, 1]
}

Hope it was helpful for you, happy coding!